Cual es el número mas grande con nombre?

Todos cuando somos niños y aprendemos los números, llega ese momento en el que nos preguntamos, y cual es el número mas grande que hay?

Bueno la respuesta es que es infinito, y quizás cuando eramos niños fue algo difícil de entender, o extraño, pero luego de resolvernos esta duda una cosa que yo si me llegue a preguntar varias veces fue que entonces cual era el mayor número con nombre, o como nombrar y o escribir esos números tan descomunales que vendrían después de lo que conocemos como millones, trillones, etc.

Antes de contestar a esta pregunta, llegar al limite de la escala numérica para nombrar números que hay, considero necesario ver antes un pequeño dato sobre esta escala y la forma de representar científicamente números grandes.

Escala numérica corta y larga:

Este dato es algo que a mi me parece bastante sorprendente, y es que el un billón es mucho mas pequeño en Estados Unidos que en la mayoría de países de América del sur y varios de América Central. Cómo es que un número valga más segun donde se este? Simple, esto va en la forma de nombrarlos, la palabra Billón varia según la escala numérica que se use.

Es bastante inconveniente esto, pero así son las cosas, entonces, que es la escala corta y la larga?

La diferencia se nota cuando llegamos al  999 millones, si añadimos un millón más, que daría? En escala corta nos da un Billón, mientras que en la escala larga a este mismo número se le nombra mil millones o millardo. Por tanto el trillon de la escala corta es el billon de la escala larga, parece poco pero hay una enorme diferencia y entre más grandes son los números más aumenta esta.

Notación científica:

La notación científica es la forma en la que se representan los números cuyas cifras son muchas, de forma que no tengamos que escribir cada una de ellas, para hacer esto se usan potencias.
Se escribe un 10 que va acompañado de una potencia, la cual en este caso representa la cantidad de cifras que tendrá el numero que queremos representar.
El método de la notación científica va mas allá de cifras cuyos números son solo un uno seguido de solo ceros y también describe números muy pequeños, pero esto lo ignoraremos ya que no es el tema a tratar.

Sabiendo esto podemos escribir los números de la siguiente manera:

\[ 10^0 = 1\\ 10^1 = 10\\ 10^2 = 100\\ •••\\ 10^6 = \text{Millón}\\ \]

Como podemos ver es mucho mas simple que poner los muchos ceros que puedan tener los números de millones, y con este método también ya sabemos como escribir números enormes, ya que solo basta imaginar cuantas cifras queremos que tenga y escribirlo en esta notación… pero ya verán como luego hasta esta notación quedara corta ante los números que aprenderemos a escribir.

«Fin» de los nombres de la escala numérica:

Bueno ya sabemos la diferencia entre la escala larga y la corta y como representar estos números de forma rápida y eficiente, pero ahora volvemos al tema inicial, cual es el último número nombrado por esta escala?

Bueno, mostraremos aqui los primeros 10 «llones» por llamarlos de alguna manera:

\[ 10^6 = \text{Millón}\\ 10^9 = \text{Millardo (Billón en escala corta)}\\ 10^{12} = \text{Billón}\\ 10^{18} = \text{Trillón}\\ 10^{24} = \text{Cuatrillón}\\ 10^{30} = \text{Quintillón}\\ 10^{36} = \text{Sextillón}\\ 10^{42} = \text{Septillón}\\ 10^{48} = \text{Octillón}\\ 10^{54} = \text{Nonillón}\\ 10^{60} = \text{Decillón} \]

Esto serian los básicos 10, como pueden observar cambia el prefijo antes de «llon» cada 6 cifras cero que se le añaden al número, por lo que si seguimos con esta regla podemos llegar a más y más alto con esto, simplemente cambiando prefijo, es mas de esta forma podemos llegar a un Vigentillón, Trigintillon y más.

Aqui lo grande que estos numeros serian

\[ 10^{120} = Vigentillón\\ 10^{180} = Trigintillón\\ •••\\ 10^{600} = Centillón\\ 10^{1200} = DuoCentillón\\ •••\\ 10^{6000} = Millinillón\\ \]

Ya estos son números descomunales, pero nos permiten ver que ya prácticamente podemos contar hasta el infinito… no?

Pues va a llegar un momento que esta nomenclatura va a ser obsoleta y los prefijos no nos van a alcanzar ya que serian muy entreverado saber el nombre, y cuando ese numero llegue podría nombrarse si, pero seria complicadisimo, y allí es donde podriamos decir los numeros han dejado de tener un nombre sistemático.

Pese a esto no es normal llegar a usar estos números, por lo que hay otras nomenclaturas para tan enormes cifras, veremos entonces el…

Gúgol:

Como dato curioso antes de ver la enormidad de las siguientes cifras, esta el hecho de que quien las nombro fue un niño de 9 años, siendo este el sobrino del matemático Edward Kasner, el cual le pidió nombrase dichos números. Sin más que decir veamoslos.

El gúgol es representada como ​\( 10^{100} \)​ osea un 1 seguido de 100 ceros, ha esta altura ya no es tan sorprendente pues el Vigentillón lo supera con 20 cifras más, pero el gúgol por mas que sea mas chico que lo anterior visto, dará pie a un numero más grande que todos los anteriores juntos.

El gúgolplex es un numero el cual consta de un 1 seguido de un gúgol de ceros representándose como\( 10^{(10^{100})} \) o \( 10^{gúgol} \)Por si fuera poco también existe un número llamado gúgolduplex que es \( 10^{gúgolplex} \) que es un 1 seguido de un gúgolplex de ceros.

Increíble no? y pues este es el último número con nombre que veremos, pero lo que sigue es aún mejor.

Antes de seguir con la escritura para números más grandes aun, otro pequeño dato curioso, es que pudo haberte sonado parecido el nombre de gúgol al del buscador Google, y es que el famoso buscados basa su nombre en el de este número, como analogía a la enorme cantidad de resultados que nos puede exponer este.

Torres de exponentes:

Luego de todo lo anterior… que números pueden ser más grandes? Y bueno pues hay infinitos números más grandes, de los cuales ya no hablaremos de nombres, sino que de representación de estos.

Así como hemos estado usando la notación científica vemos que podemos crear números gigantescos, pues con esto de elevar números existe lo que se llama torre de exponentes, lo cual consta de elevar números a números elevados a otros numeros, de forma que el resultado sea gigantesco, así como hicimos con el gúgol.

El truco aquí esta en como se realiza la operación, ya que no es lo mismo \( 10^{(10^{100})} \) (un gúgolplex) que ​\( (10^{10})^{100} \)​ en el primero serán un gúgol de cifras, mientras que en el segundo, serán muchos menos.

Figuras geométricas?

Aquí es donde las cosas realmente se saldrán de control, la notación que vamos a utilizar se llama notación Steinhaus–Moser y consiste en usar figuras geométricas para elevar números varias veces.

Esta notación consiste de la figura y el numero, el cual estará dentro de esta. Y se rige por las siguientes 2 normas:

1. Un número dentro de un triangulo es igual a ese número elevado a si mismo   = \( n^n \)
2. Las figuras de más de 3 lados significa que el número dentro de esta se encuentra encerrado en su misma cantidad de figuras con un lado menor al la figura inicial Ej:   representa a un 2 dentro de 2 triángulos, los cuales siguen ambos la regla 1

Se ve muy inofensivo esto y que no llegaremos muy lejos, pero hagamos la prueba usando de ejemplo  :

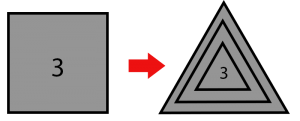
Al hacer el primer triangulo seria 3³ que es 27, el segundo daría \( 27^{27} \) que es un numero ya muy grande, finalmente aún estaría dentro de un triángulo por lo que nos quedaría ​\( (27^{27})^{(27^{27})} \)​ este número cuenta con millones y millones de cifras, aunque lo interesante llega cuando consideramos que pasa si en ves de poner un 3 en un cuadrado lo hacemos en un pentágono :

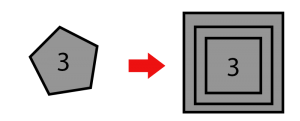
3 pentagono es 3 dentro de 3 cuadrados, el primer cuadrado ya sabemos que vale \( (27^{27})^{(27^{27})} \), así que lo colocaremos dentro de los 2 cuadrados:

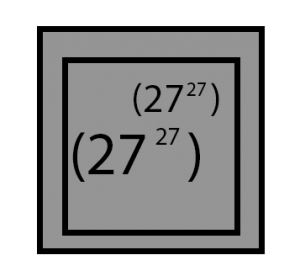
Llegados a este paso nos es imposible seguir, ya que ese numero que ya de por si es enorme hay que encerrarlo dentro de ese numero de triangulos!!! que por cada triangulo se va volviendo mas grande de forma descomunal… y sin mencionar que seguirá dentro de un ultimo cuadrado.
Este número supera por lejos todos los anteriores con tantas cifras que ni siquiera podemos darle nombre al numero de cifras que tiene, y eso que solo se necesito un 3 y un pentagono.

Para cerrar este articulo los dejaré con un ejercicio mental que los dejara pensando lo descomunal que puede llegar a formarse mediante esta forma de representarlos y son tan grandes que ya ni siquiera hacerse una idea de su magnitud podemos, he aquí el ejercicio mental:

Piensen en ese numero y tomen en cuenta que ya de por si esta en un octágono, por lo que esta dentro de gúgolduplex heptágonos, hexagonos, cuadrados y triangulos y que asi seguirá desarmandose teniendo luego un numero descomunal de triangulos y demas figuras que se desarmaran guglillones y guglillones y  gúgoldupleximas veces… simplemente magnifico.

Ejemplos de números colosales en  algo cotidiano como lo son los juegos:
Numeros Colosales en Juegos.

Y que te han parecido estos números?
Coméntanos aquí abajo en los comentarios 🙂