Cuantos habrán visto, jugado y/o resuelto un cubo de Rubik, cuantos han jugado al ajedrez o al 3 en rata, ta te ti, gato o como se llame en tu país. Estos juegos tienen algo en común, y esto es que existe una cantidad de combinaciones máxima en ellos, hay una cantidad finita de partidas del 3 en raya, como también de partidas de ajedrez o movimientos posibles dentro de un cubo de Rubik, y ya veras lo grande que pueden llegar a ser.

3 en raya / Ta te ti / gato

Bueno este clásico juego como ya sabrán consta de colocar cruz o circulo hasta que alguien haga una linea ya sea diagonal, horizontal o vertical, pero cuantas posibles jugadas hay? Básicamente considerando que muchos de los movimientos son idénticos solo con cambiar el punto de vista del tablero los movimientos son menos de los que aparentan, pero para esta ocasión ignoraremos esto, ya que lo que queremos mostrar son números enormes. Si tomamos como que cada movimiento no se repite y que el juego termina en empate llenando todo el tablero, entonces tendríamos que inicialmente el primer jugador tendría 9 opciones de jugada, una en cada espacio en blanco, al realizar la jugada su contrincante tendría 8 jugadas ya que uno de los espacios fue marcado, al siguiente turno serian 7… y así se irían reduciendo las posibilidades hasta llegar a 0 espacios disponibles. Esto calculado mediante combinatoria nos da 9! (9 factorial), numero que representa la multiplicación de 9 por todos los enteros anteriores (9x8x7x… hasta llegar al 1). Escrito cifra por cifra esto seria: 362880 jugadas posibles.
Este número no es tan sorprendente, pero no deja de ser un número grande, ahora veremos como los otros 2 números no tienen ni comparación con este de lo grandes que son… este fue solo un calentamiento.

Cubo de Rubik

Aquí es donde las cosas se pondrán realmente interesantes, y es que este grandioso cubo cuenta con mas combinaciones de las que te estarás imaginando, veamos cuantas son y por que. El cubo cuenta con 8 aristas, esto nos lleva a 8! posibles movimientos, que si bien es menos que lo anterior visto (40320) ya verán como este numero crecerá conforme agreguemos las demás reglas y cualidades del cubo.
Estas aristas mencionadas con anterioridad también pueden tener 3 orientaciones diferentes, lo cual multiplica 3 veces la cantidad de movimientos, pero 3 veces por cada una de las aristas, por tanto esto es ​\( 8!\text{ x }3^8 \)​ numero que resulta ser mas de 200 millones.
Repitiendo el proceso anterior con las aristas obtendremos que son 12 aristas con 2 posibles orientaciones que dan ​\( 12!\text{ x }2 \)​ movimientos, estos 2 resultados anteriores deben multiplicarse… Ese numero seria increíblemente alto, si no fuera por una pequeña condición, y es que el cubo tiene sus movimientos simétricos a otros, como en el juego anterior, que en este caso si los contaremos, lo cual nos dividiría entre 12 los movimientos anteriores calculados, nos terminaría quedando la siguiente cuenta:

\[ \frac{8!\text{ x }3^8\text{ x }12!\text{ x }2}{12} \]

Resultando en mas de 43 trillones!! que con todas sus cifras seria 43.252.003.274.489.856.000 de posibles movimientos.
Esto resulta ser tanto que si se apilara un cubo arriba de otro formando una torre por cada posible movimiento del cubo, esta torre llegaría a  la constelación Columba que se encuentra a una distancia de 261 años luz!!.

Sudoku

Este juego, tiene mas cifras que el anterior, y es que esto se debe a que consta de menos restricciones y más cuadrados que un cubo de rubik. Sus combinaciones fueron resueltas por maquina debido a los problemas de las restricciones de este juego, el resultado final resultó ser mayor a 6 mil trillones superando por lejos los 43 trillones del cubo rubik. El numero colosal de combinaciones de sudoku cifra por cifra vendría siendo el siguiente 6.670.903.752.021.072.936.960.

Ajedrez

Lo mejor siempre para lo último y es que si los números anteriores te impresionaron, este lo hará muchísimo más, y es que los ya vistos son ridículamente pequeños en comparación… no me crees? Pues empecemos a hacer las cuentas.
Primero que nada veamos una pequeña demostración de lo impresionante que puede llegar a ser:

Se cuenta que el inventor de este juego se lo regalo al rey para que pudiera divertirse jugandolo, al rey el juego le fascino y a cambio le dijo a su creador que a cambio le daría lo que el desee, este no quería nada a cambio pero ante la insistencia del rey a que pidiera algo este le pidió que por la primer casilla del tablero le diera una semilla de trigo, el doble por la segunda, el cuatropea por la tercera y así hasta la ultima. El rey accedio, pensando que era poco y el siendo tan rico podría dárselo, pues fue un grave error, luego de los cálculos el rey debía más de 18 trillones de semillas de trigo, más trigo del que habia en el mundo, el inventor no reclamo su ceuda sino que la uso para enseñar una lección al rey.

El número de la historia contada es bastante menor al visto arriba en el sudoku si, pero estamos hablando solo de un resultado dado por las 64 casillas y no de sus combinaciones con cada una de las piezas ni sus movimientos ni las reglas de juego, así que podemos ver que de aquí pueden salir números más que enormes.
Ya las primeras 10 jugadas posibles son 165 cuatrillones y medio, número que ya supera por mucho a los anteriores, y recuerden, seguimos en las primeras 10 jugadas.
El primero en calcular esta cantidad inmensa de posibilidades fue Claude Shannon el cual dio con el número de Shannon como respuesta al problema, el cual tiene este nombre como único nombre, ya que es tan grande que se sale de la escala de millones, trillones y demas terminos que solemos usar. Representado como ​\( 10^{120} \)​ lo cual implica un 1 seguido de 120 ceros. Si así de colosal es, es más el universo observable consta de ​\( 10^{81} \)​ átomos aproximadamente, si hay mas jugadas de ajedrez que átomos en el universo hasta ahora conocido. Y eso que una persona promedio de 70 kg posee aproximadamente \( 6,7^{27} \) átomos en su cuerpo.
Es impresionante porque ya los números con los que tratamos no poseen ni nombre ni son concebibles para la imaginación humana… pero esto no a acabado aquí. Impresionante no?
El número de Shannon hay cosas que no tiene en cuenta por lo que si hacemos unos mejores cálculos y añadimos algunas otras de las posibles acciones y movimientos que una pieza puede tener llegamos a la cifra de

\[ 10^{100.000} \]

 que si, es un 1 seguido de 100.000 ceros esto ya supera por muchas veces la cantidad de átomos del universo observable y si antes no podíamos ni imaginar la magnitud de los números a tratar ahora mucho menos, pero oh sorpresa… esta no es la mejor versión del calculo de las combinaciones, hay una mucho mayor.
El actual mejor resultado de la cantidad de posibles jugadas de ajedrez actualmente (si aun puede aumentar debido a reglas, terminación prematura de la partida, peones que llegan al otro extremo etc) es el resultado hallado por Godfrey Harold Hardy, el cual llego a la impresionante cifra de ​\( 10^{(10^{50})} \)​ lo cual representa un 1 seguido de ​\( 10^{50} \)​ ceros, numero el cual es un 1 seguido de 50 ceros. Numero que ya es ridículamente grande que ni podemos entender lo grande que es.

Quieres saber como nombrar números así de grandes? Este articulo puede interesarte:
Cómo escribir/nombrar números gigantescos.

Y a ti qué te han parecido estos números tan descomunales? Qué juego te gusta mas de estos 4?
Háznoslo saber en los comentarios 🙂

Cual es el número mas grande con nombre?

Todos cuando somos niños y aprendemos los números, llega ese momento en el que nos preguntamos, y cual es el número mas grande que hay?

Bueno la respuesta es que es infinito, y quizás cuando eramos niños fue algo difícil de entender, o extraño, pero luego de resolvernos esta duda una cosa que yo si me llegue a preguntar varias veces fue que entonces cual era el mayor número con nombre, o como nombrar y o escribir esos números tan descomunales que vendrían después de lo que conocemos como millones, trillones, etc.

Antes de contestar a esta pregunta, llegar al limite de la escala numérica para nombrar números que hay, considero necesario ver antes un pequeño dato sobre esta escala y la forma de representar científicamente números grandes.

Escala numérica corta y larga:

Este dato es algo que a mi me parece bastante sorprendente, y es que el un billón es mucho mas pequeño en Estados Unidos que en la mayoría de países de América del sur y varios de América Central. Cómo es que un número valga más segun donde se este? Simple, esto va en la forma de nombrarlos, la palabra Billón varia según la escala numérica que se use.

Es bastante inconveniente esto, pero así son las cosas, entonces, que es la escala corta y la larga?

La diferencia se nota cuando llegamos al  999 millones, si añadimos un millón más, que daría? En escala corta nos da un Billón, mientras que en la escala larga a este mismo número se le nombra mil millones o millardo. Por tanto el trillon de la escala corta es el billon de la escala larga, parece poco pero hay una enorme diferencia y entre más grandes son los números más aumenta esta.

Notación científica:

La notación científica es la forma en la que se representan los números cuyas cifras son muchas, de forma que no tengamos que escribir cada una de ellas, para hacer esto se usan potencias.
Se escribe un 10 que va acompañado de una potencia, la cual en este caso representa la cantidad de cifras que tendrá el numero que queremos representar.
El método de la notación científica va mas allá de cifras cuyos números son solo un uno seguido de solo ceros y también describe números muy pequeños, pero esto lo ignoraremos ya que no es el tema a tratar.

Sabiendo esto podemos escribir los números de la siguiente manera:

\[ 10^0 = 1\\ 10^1 = 10\\ 10^2 = 100\\ •••\\ 10^6 = \text{Millón}\\ \]

Como podemos ver es mucho mas simple que poner los muchos ceros que puedan tener los números de millones, y con este método también ya sabemos como escribir números enormes, ya que solo basta imaginar cuantas cifras queremos que tenga y escribirlo en esta notación… pero ya verán como luego hasta esta notación quedara corta ante los números que aprenderemos a escribir.

«Fin» de los nombres de la escala numérica:

Bueno ya sabemos la diferencia entre la escala larga y la corta y como representar estos números de forma rápida y eficiente, pero ahora volvemos al tema inicial, cual es el último número nombrado por esta escala?

Bueno, mostraremos aqui los primeros 10 «llones» por llamarlos de alguna manera:

\[ 10^6 = \text{Millón}\\ 10^9 = \text{Millardo (Billón en escala corta)}\\ 10^{12} = \text{Billón}\\ 10^{18} = \text{Trillón}\\ 10^{24} = \text{Cuatrillón}\\ 10^{30} = \text{Quintillón}\\ 10^{36} = \text{Sextillón}\\ 10^{42} = \text{Septillón}\\ 10^{48} = \text{Octillón}\\ 10^{54} = \text{Nonillón}\\ 10^{60} = \text{Decillón} \]

Esto serian los básicos 10, como pueden observar cambia el prefijo antes de «llon» cada 6 cifras cero que se le añaden al número, por lo que si seguimos con esta regla podemos llegar a más y más alto con esto, simplemente cambiando prefijo, es mas de esta forma podemos llegar a un Vigentillón, Trigintillon y más.

Aqui lo grande que estos numeros serian

\[ 10^{120} = Vigentillón\\ 10^{180} = Trigintillón\\ •••\\ 10^{600} = Centillón\\ 10^{1200} = DuoCentillón\\ •••\\ 10^{6000} = Millinillón\\ \]

Ya estos son números descomunales, pero nos permiten ver que ya prácticamente podemos contar hasta el infinito… no?

Pues va a llegar un momento que esta nomenclatura va a ser obsoleta y los prefijos no nos van a alcanzar ya que serian muy entreverado saber el nombre, y cuando ese numero llegue podría nombrarse si, pero seria complicadisimo, y allí es donde podriamos decir los numeros han dejado de tener un nombre sistemático.

Pese a esto no es normal llegar a usar estos números, por lo que hay otras nomenclaturas para tan enormes cifras, veremos entonces el…

Gúgol:

Como dato curioso antes de ver la enormidad de las siguientes cifras, esta el hecho de que quien las nombro fue un niño de 9 años, siendo este el sobrino del matemático Edward Kasner, el cual le pidió nombrase dichos números. Sin más que decir veamoslos.

El gúgol es representada como ​\( 10^{100} \)​ osea un 1 seguido de 100 ceros, ha esta altura ya no es tan sorprendente pues el Vigentillón lo supera con 20 cifras más, pero el gúgol por mas que sea mas chico que lo anterior visto, dará pie a un numero más grande que todos los anteriores juntos.

El gúgolplex es un numero el cual consta de un 1 seguido de un gúgol de ceros representándose como\( 10^{(10^{100})} \) o \( 10^{gúgol} \)Por si fuera poco también existe un número llamado gúgolduplex que es \( 10^{gúgolplex} \) que es un 1 seguido de un gúgolplex de ceros.

Increíble no? y pues este es el último número con nombre que veremos, pero lo que sigue es aún mejor.

Antes de seguir con la escritura para números más grandes aun, otro pequeño dato curioso, es que pudo haberte sonado parecido el nombre de gúgol al del buscador Google, y es que el famoso buscados basa su nombre en el de este número, como analogía a la enorme cantidad de resultados que nos puede exponer este.

Torres de exponentes:

Luego de todo lo anterior… que números pueden ser más grandes? Y bueno pues hay infinitos números más grandes, de los cuales ya no hablaremos de nombres, sino que de representación de estos.

Así como hemos estado usando la notación científica vemos que podemos crear números gigantescos, pues con esto de elevar números existe lo que se llama torre de exponentes, lo cual consta de elevar números a números elevados a otros numeros, de forma que el resultado sea gigantesco, así como hicimos con el gúgol.

El truco aquí esta en como se realiza la operación, ya que no es lo mismo \( 10^{(10^{100})} \) (un gúgolplex) que ​\( (10^{10})^{100} \)​ en el primero serán un gúgol de cifras, mientras que en el segundo, serán muchos menos.

Figuras geométricas?

Aquí es donde las cosas realmente se saldrán de control, la notación que vamos a utilizar se llama notación Steinhaus–Moser y consiste en usar figuras geométricas para elevar números varias veces.

Esta notación consiste de la figura y el numero, el cual estará dentro de esta. Y se rige por las siguientes 2 normas:

1. Un número dentro de un triangulo es igual a ese número elevado a si mismo   = \( n^n \)
2. Las figuras de más de 3 lados significa que el número dentro de esta se encuentra encerrado en su misma cantidad de figuras con un lado menor al la figura inicial Ej:   representa a un 2 dentro de 2 triángulos, los cuales siguen ambos la regla 1

Se ve muy inofensivo esto y que no llegaremos muy lejos, pero hagamos la prueba usando de ejemplo  :

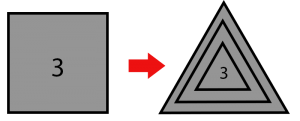
Al hacer el primer triangulo seria 3³ que es 27, el segundo daría \( 27^{27} \) que es un numero ya muy grande, finalmente aún estaría dentro de un triángulo por lo que nos quedaría ​\( (27^{27})^{(27^{27})} \)​ este número cuenta con millones y millones de cifras, aunque lo interesante llega cuando consideramos que pasa si en ves de poner un 3 en un cuadrado lo hacemos en un pentágono :

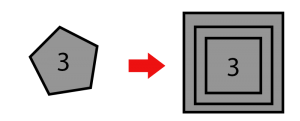
3 pentagono es 3 dentro de 3 cuadrados, el primer cuadrado ya sabemos que vale \( (27^{27})^{(27^{27})} \), así que lo colocaremos dentro de los 2 cuadrados:

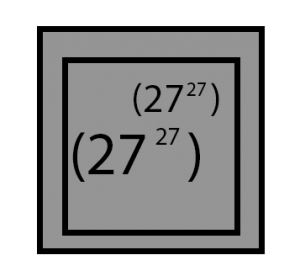
Llegados a este paso nos es imposible seguir, ya que ese numero que ya de por si es enorme hay que encerrarlo dentro de ese numero de triangulos!!! que por cada triangulo se va volviendo mas grande de forma descomunal… y sin mencionar que seguirá dentro de un ultimo cuadrado.
Este número supera por lejos todos los anteriores con tantas cifras que ni siquiera podemos darle nombre al numero de cifras que tiene, y eso que solo se necesito un 3 y un pentagono.

Para cerrar este articulo los dejaré con un ejercicio mental que los dejara pensando lo descomunal que puede llegar a formarse mediante esta forma de representarlos y son tan grandes que ya ni siquiera hacerse una idea de su magnitud podemos, he aquí el ejercicio mental:

Piensen en ese numero y tomen en cuenta que ya de por si esta en un octágono, por lo que esta dentro de gúgolduplex heptágonos, hexagonos, cuadrados y triangulos y que asi seguirá desarmandose teniendo luego un numero descomunal de triangulos y demas figuras que se desarmaran guglillones y guglillones y  gúgoldupleximas veces… simplemente magnifico.

Ejemplos de números colosales en  algo cotidiano como lo son los juegos:
Numeros Colosales en Juegos.

Y que te han parecido estos números?
Coméntanos aquí abajo en los comentarios 🙂

Se puede morir… riendose?

Si, si se puede y te traemos aquí las historias de aquellos que por desgracia, o  mejor dicho, por la gracia que les habrá tenido que dar a estas personas para que esa misma gracia los haya matado a las carcajadas.

Crisipo de Solos y el Burro

Durante las épocas antes de Cristo, siglo II a.c para ser mas exactos, un Filosofo Griego llamado Crisipo de Solos tuvo la idea de dar de beber vino a su burro. Hecho esto el burro quedo borracho e intento comer unos higos, o peras según algunas versiones, lo cual al moverse mas tontamente por el efecto del alcohol hizo que el filosofo empezara a reir a carcajadas, hasta que finalmente murió… probablemente la primera persona en la historia de la humanidad en morir de esta forma, pero quien sabe.

El rey Birmano

Se cuenta que en 1995 un cierto rey de Birmania hablando con un mercader italiano se enteró por cuenta de este que en Venecia se vivía en un estado libre, el cual no poseía un rey, esta idea se le hacia muy disparatada a este rey, el cual según cuenta esta historia murió allí mismo de la risa que le provocó esto… no sabemos si en verdad haya ocurrido o no, pero no deja de ser una historia curiosa y el como a un rey podría parecerle disparatada la idea de un estado libre.

La opera mortal

Corría el año 1782, y nuestra protagonista la señorita Fitzherbert había ido a ver una obra de teatro llamada The Beggar’s la cual era de opera. En cierto momento apareció Charles Bannister quien participaba de la obra caracterizado como el personaje Peachum. Esto le causo risa tal que la sacaron del teatro ya que sus carcajadas eran tan fuertes que molestaban a los demás, sin embargo ella seguía riendo. La señorita rió por el resto de la noche para finalmente morir a las risas la mañana siguiente.

El adivino

Esta historia nos presenta a un adivino, el cual decía haber predicho la fecha y hora de su muerte, al llegar la hora de la verdad, el seguía vivo… como es que esta aquí? pues bueno, verán, el hecho de seguir vivo le dio mucha alegría, empezó a reír y reír y ya saben como acaba esto, le dio un infarto, bastante irónico no?

The Goodies

Tienes un programa de TV favorito? Alex Mitchell también lo tenia, «The Goodies» un dia de 1975 estaba viendo el cual supongo habrá sido hasta antes de morir su episodio favorito llamado «Kung Fu Kapers». Una escena la cual mostraba una pelea graciosa le causo la muerte por infarto.
Lo màs curioso es que la esposa de Alex ya viuda decidió mandar una carta al elenco del programa, agradeciendoles… no que mataran a su esposo… sino que sus ultimos momentos de vida hayan sido entre risas.
El episodio lo pueden buscar por Internet si quieren verlo, pero bueno ya saben, con cuidado que esta para morirse de risa, literalmente hablando.

El sueño chistoso

Ocurrida en 2003 esta historia nos cuenta la historia de un hombre de 52 años, el cual estaba tranquilamente durmiendo con  su esposa hasta que en sueños empezó a reír. Ya sabrán a donde va esto, la esposa se despertó por las fuertes carcajadas, el esposo estaba dormido pero no paraba de reír, trato de despertarlo pero fue inútil. A los 2 minutos de risa dejo de reír para siempre.

Bueno luego de todo esto ya sabemos que posible es, y bueno muchos cuando nos reímos demasiado sentimos a veces cierto dolor en las costillas o en alguna otra zona, pero uno no piensa que pueda morir por eso.
Hilaridad Fatal es el nombre clínico para cuando se muere de esta forma, y como estos màs casos hay, en los cuales lo màs común es morir por asfixia, embolia cerebral, rupturas en venas y/o arterias y ataques cardíacos.

Y que opinas tu? este post te ha dejado muerto de risa? Dinoslo en los comentarios.

El universo, es tan grande y colosal, es todo lo que nos rodea y en donde se encuentra todo lo que conocemos Pero… tendrá final el universo?

Aunque el futuro del universo es incierto, lamentablemente la respuesta parece ser que sí, te preguntaras como algo tan inmenso puede dejar de existir, pues no necesariamente debe dejar de existir para que llegue a su fin, hay otras formas:

Big Crunch:

(La gran implosión)

La teoría del Big Crunch indicaría que el universo iría disminuyendo paulatinamente su expansión hasta detenerse esta por completo. Seguido esto de una deceleración, osea que empezaría a colapsar a un solo punto, en el cual se juntaría toda la materia que existe… Para este punto es probable que lo halles familiar, y es que es algo inverso al Big Bang, para que luego se genere un nuevo universo.
La teoría también explica que el universo luego de ese Big Bang seguiría el ciclo, renaciendo y muriendo el universo por el resto de la eternidad.
A este tipo de universo que cumple este ciclo de Big Bang y Big Crunch se le llama teoría del Universo Oscilante o Big Bounce, por razones obvias.
Pese a todo esto, la teoría no se ve muy probable en la practica, esto debido a que las observaciones apuntan a que lejos de desacelerar, el universo aumenta cada vez más y más su expansión. Y por si fuera poco, el universo oscilante entra en contradicción con las leyes físicas, (principalmente la 2° ley de la termodinámica, la cual a grosso modo explica que los fenómenos físicos son irreversibles, en este caso volver al big bang) para arreglar esto se cree que durante el proceso de colapso el tiempo podría ir hacia atrás, o que las leyes físicas fueran cambiando entre cada oscilación.
El momento en el cual el universo llegaría a detenerse y comenzar con el colapso esta definido por la densidad critica de universo, siendo esta la cual determina el tipo de universo, de ser muy baja esta densidad, el universo estaría en una expansión perpetua, y el Big Crunch no podría darse nunca.

Big Freeze

(Gran congelación, o gran susurrante)

Como mencionamos arriba si la densidad critica del universo es lo suficientemente baja, este se expandirá indefinidamente, y es que estamos hablando de un tipo distinto de universo, lo cual conlleva un final diferente, la gran congelación.
En esta versión del fin del universo, lejos de terminar por un colapso llega a su fin por su expansión indefinida, debido a la ya antes mencionada 2° ley de la termodinámica, esta vez debiéndose a que la energía del universo iría disminuyendo hasta finalmente agotarse. Agotarse en una forma metafórica, ya que las leyes de la física dicen que la energía no se destruye ni se crea, sino que solo se transforman en otras energías. Pero debido a que el calor y demás energías se disiparían indefinidamente, llegaría un punto en el que ya no seria posible transformarla, sigue allí, pero no puede moverse nada, lo cual lleva el nombre de muerte térmica del universo.
Antes de llegar a esto, las galaxias se irían separando unas de otras, quedando como «islas galácticas» por llamarlo de alguna manera, para luego en una siguiente era, solo quedaran los restos de lo que fueron las estrellas y demás cuerpos presentes en el universo, los protones y neutrones desaparecerían con el correr de los años y los últimos en morir serian los agujeros negros debido a la radiación de Hawking.
El universo seguiría en expansión pero dentro de el todo seria inmóvil, como si de una colosal foto se tratase.
Es bastante escalofriante pensar en que todo estaría sumergido en temperaturas tan bajas, que llegan al cero absoluto (temperatura mínima que existe) y que nada podrá moverse por el resto de la eternidad. Pero de no ser así también se cree que podría dar pie a 2 distintos posibles futuros fines del universo más, el primero es el Big Crunch mencionado arriba, el cual se generaría tras muchísimo tiempo después al desaparecer la energía oscura, la cual impide la deceleración del universo. Y el otro fin del universo al cual da pie es al…

Big Rip

El Big Rip (Gran desgarro) nos cuenta como el universo, también del tipo que tiene expansión indefinida podría  en vez de llegar a la muerte térmica del universo, podría desgarrarse. Para entenderlo retomemos la idea de las «islas galácticas» estas surgían de que las galaxias se separaban más y más entre ellas, esto debido a que la energía oscura, la cual vimos evita el universo decelere, pero no solo hace eso esta es también la que hace que acelere cada vez más, de ser así y si sigue acelerándose de tal manera llegaría un punto en el cual dentro de cada galaxia los sistemas solares y los planetas se vayan separando entre sí debido a que la gravedad no podría mantenerlos juntos. Esto seria así hasta llegar a nivel atómico, momento en el cual cada átomo se desprendería de los demás y a su vez estos se desgarrarían y posteriormente transformarían en radiación.
Todo el universo reducido a radiación y nada más, esta teoría no daría lugar a que pudiera ocurrir ningún tipo de «restaurador del universo» como ocurriría en la teoría oscilante del universo.

Estas ultimas 2 teorías son las mas escalofriantes pero son las que tienen más fundamento y las mas probables hasta ahora.
Pero descuida, aunque el universo tiene fin, los años que faltan para que pase algo de tal magnitud son tantos que ninguno de nosotros estará ya para ese entonces.

Sabias que la lengua española cuenta con más de 280 mil palabras?

Es fascinante, pero resulta ser que de tantas palabras que hay la persona promedio solo usa cerca de 300 de esas palabras, de allí surgió la idea de #LaPalabraDelDia. Idea la cual pretende dar a conocer palabras  al azar de nuestro rico lenguaje, y poner sus definiciones, dando a conocer palabras que quizás no conocías, para que puedan usarlas, o para simplemente expandir su vocabulario que nunca vine a mal.

• Bizarro: Alguien que es valiente o apuesto.
• Enervante: Cuando algo hace sentir muchos nervios, o cuando debilita y/o hace sentir que se pierden las fuerzas.
• Ignaro: Sinónimo de ignorante.
• Descerrajar: Es la acción de forzar o arrancar una cerradura con violencia, o el disparar a alguien a quemarropa con un arma de fuego.
• Plañir: Es sollozar, llorar o gemir al lamentarse algo.
• Badajear: Es hablar mucho, y que a su vez solo se estén diciendo tonterías.
• Fronda: Es un conjunto de hojas o ramas, un sinónimo de follaje.
• Hojarasca: Refiere a la frondosidad de algunos arboles, o a las hojas secas que han caído de estos. Como también puede usarse para hablar sobre alguna cosa que sea inútil o de escasa importancia.
• Suplicio: Sufrimiento causado por la espera de algo que no llega, también puede referir a un gran sufrimiento moral, o a algo muy molesto. También tiene como significado el ser un castigo físico y/o pena de muerte.
• Frondosidad: Refiere a la abundancia de hojas y ramas, como también puede hacer referencia a algo que es frondoso.
• Lozanía: Referido a las plantas cuando éstas muestran verdor en su aspecto y frondosidad.
• Ebúrneo: Que es de marfil o tiene aspecto similar a este.
• Gibar: Fastidiar o molestar.
• Circunspecto: Que es serio o actúa de esta forma, que actúa con prudencia o cautela.
• Nefelibato: Es una persona que «anda en las nubes» o anda bastante distraído en sus pensamientos.
• Ringla: Se puede decir así así a una fila o hilera de cosas.
• Retozar: Acción de saltar y brincar alegremente, o también se le dice así a la practica de juegos amorosos.
• Triscar: Retozar o juguetear aunque también puede significar el hacer ruido con los pies.
• Trolero: Una persona mentirosa y/o embustera.
• Idílico: es algo utópico o que esta excesivamente idealizado.
• Oxear: Se dice así a la acción de espantar a las aves domésticas.
• Noctívago: Refiere a algo o alguien que vaga por las noches.
• Saporífero: Es aquello que causa o da dolor.
• Rauco: Sinónimo de afónico o ronco.
• Tesela: Se llama así a cada una de las piezas que compone un mosaico.
• Abstruso: Cualquier cosa cuya comprensión sea difícil.
• Bahúno: Es la persona que es soez, ordinaria, vil o ruin.
• Lenguaraz: Persona que habla y domina más de 2 idiomas.
• Impetrar: Cuando se consigue algo que se quiere por medio del ruego.
• Giste: Este es el nombre que recibe la espuma de la cerveza.
• Acmé: Es el momento culminante y de mayor intensidad de algo… referido mayormente al momento más intenso de una enfermedad.
• Estulticia: Es sinónimo de necedad, ignorancia y estupidez, se llama estulto a el que posee estas características.
• Inopia: Indigencia, pobreza, escasez. Aunque también puede usarse la frase «Estar en la inopia» para referirse a la acción del ignorar algo que otros conocen, o el no haberse enterado de ello.
• Babieca: Persona que carece de inteligencia.
• Ablación: Es la extirpación de una parte del cuerpo.
• Facineroso: Persona malvada y de condición perversa.
• «Apapachar»: Es una reduplicación de la palabra «apachar», la cual viene del náhuatl «patzoa», cuyo significado es el de dar apapachos a alguien.
• Invectiva: Es un discurso o escrito de carácter agresivo o que va contra personas o cosas.
• Badila: Refiere a una ironía o sarcasmo, el cual cumple la función de disimular un agravio hacia alguien.
• Verbigracia: Sinónimo de la frase «Por Ejemplo».
• Perorata: Discurso o charla que es muy largo y aburrido.
• Domeñar: Sinónimo de las palabras dominar y someter.
• Pocotón: Es un coloquialismo Venezolano usado para expresar una gran cantidad de algo.
• Abolengo: Dirigido hacia personas, refiere a la ascendencia de estas, en especial si es ilustre.
• Letífico: Todo aquello que alegra, anima o estimula.
• Serendipia: Cuando buscando algo  te llevas la sorpresa y suerte de encontrar algo distinto a lo que buscabas.
• Exuberante: Que posee una gran cantidad de algo. (personas , objetos)
• Sempiterno: Que tiene un comienzo, pero no tiene un final, o al menos no parece tenerlo.
• Nadería: Frases que carecen de importancia y/o sentido.
• Dádivas: Regalo que se hace sin esperar nada a cambio, es dadivoso quien hace acciones de este tipo.
• Parco: Es la alguien poco soberbio, y que se modera en su accionar.
• Inefable: Es algo tan maravilloso, y que impresiona de manera tal, que no tienes palabras para describirlo… ahora si la tienen.
• Cutre: Es algo de calidad baja, descuidado o miserable.
• Exasperante: Que molesta y/o irrita mucho, algo así como la desesperación pero en molestia.
• Ósculo: Sinónimo de beso, aunque también puede referirse a las bocas o aberturas de las esponjas marinas.
• Vilipendio: Es un acto de humillación y/o denigratorio grave hacia otra persona.
• Conspicuo: Es una persona que sobresale en algo, o goza de ciertos privilegios.
• Anhelo: Deseo vehemente y muy intenso sobre algo.
• Fatuo: Es la persona que es vanidosa, engreída, y también el  necio o torpe.
• Vehemente: Acción que se hace con ímpetu y pasión, o lo que se deja llevar por esta última.
• Ímpetu: Movimiento brusco, fuerte y/o acelerado con el que se hace algo, también referido a la energía con la cual se realiza la acción.
• Frugal:  Que es en cantidad pequeña o liviano (va referido a las comidas).
• Impío: Es aquel que no tiene respeto por lo religioso, o que no muestra piedad.
• Taciturno: Que es de caracter callado, tranquilo o silencioso.

Quién no ha jugado alguna vez al clásico y famosísimo juego Pac-Man?

Un juego que formó parte de la niñez de muchos de nosotros. Un juego que era interminable y nos hacia comer y comer puntos evadiendo a fantasmas hasta perder eventualmente.

Lo que no muchos saben es que el juego en sus inicios si contaba con un último nivel, ya que debido a un error, el cual hacia que pasado el nivel 255 la pantalla quedaba de la siguiente manera:

Volviéndose imposible para el jugador seguir la partida, y se preguntaran, esto que tiene que ver con la partida legendaria de Pac-Man? Pues mucho, ya que esto es lo que hace posible que exista una partida Perfecta ya que al haber un ultimo nivel, hay un puntaje máximo a alcanzar, y es aquí que les presentamos a Billy Mitchell, reconocido por haber logrado el puntaje máximo que se pudiese conseguir dentro de este juego.

William James “Billy” Mitchell tras 6 horas de juego y con el uso de una sola vida logró el puntaje Perfecto de Pac-Man, logrando esta insuperable hazaña el 4 de julio de 1999 , instaurando lo que fue el nuevo Record Mundial y definitivo de 3.333.360 puntos.

Para lograr esto es necesario llegar al nivel 255 y a la vez conseguir cada fruta especial y comerse a cada fantasma, en cada uno de los niveles.

Pero Billy no solo posee el récord máximo de Pac-Man, sino que también consigio otros récords en los siguientes juegos:

Donkey Kong Jr. (957.300 puntos)
Donkey Kong (1.050.200 puntos)
BurguerTime (7.881.050 puntos)
Centipede (10.774.191 puntos)
Ms. Pac-Man (703.560 puntos)

Que si bien no son mundiales si son puntajes increíbles y que en su momento algunos llegaron a ser mundiales.

Para mas récords así o para ver récords más actuales de juegos puedes visitar la pagina http://www.twingalaxies.com/ la cual es el equivalente a los récords Guinnes pero solo de videojuegos.

Y tu? que tan bueno eres para jugar Pac-Man?